教科書を開いた瞬間、目に飛び込んでくるという謎の記号列。これを見ただけで「うっ」と本を閉じたくなりませんか?でも、安心してください。実はこれ、皆さんが普段仕事や生活で見慣れている「あるもの」を、数学の言葉でカッコつけて書いただけなんです。まずはこの記号アレルギーを、「日本語への翻訳」で完全に取り除くところから始めましょう。
行列の定義:「数式」を「日本語」にしてみよう
教科書の定義 A=(aij)A = (a_{ij}) の正体は「住所付きのマンション」
まず結論から言うと、教科書に出てくるという記号は、「マンションの部屋番号」と同じ意味です。
なぜなら、行列というのはただ数字をでたらめに並べているのではなく、「どの場所にある数字か」を正確に指定する必要があるからです。マンションで言えば、「階の $j$ 号室」と言えば特定の部屋が決まるのと同じで、行列も「行目の列目」と言えば、たった一つの数字が特定できます。
例えば、上の図を見てください。や というのは、計算式ではなく「1行目の1番目」「1行目の2番目」という**「住所」**を表しているに過ぎません。難しそうな記号に見えますが、「ここは3階の2号室だな」と確認する感覚で眺めればOKです。
翻訳すると「ただのデータ表(スプレッドシート)」である
行列を一言で「翻訳」すると、「Excelから、罫線を消してカッコで囲ったもの」になります。
その理由は、行列が生まれた背景に「大量のデータを整理して扱いたい」という目的があるからです。1つや2つの数字ならそのまま書けばいいですが、何十、何百というデータになると、表形式にしないと訳がわからなくなりますよね。
実際に、テストの点数表を思い浮かべてみてください。「国語・数学・英語」の点数が横に並び、「A君・Bさん・C君」のデータが縦に並んでいる。この「表」の見た目を少し数学っぽく整理したものが行列です。つまり、普段から「行列的なもの」を日常的に使いこなしているというわけです。
「行」と「列」の覚え方(漢字の作りで解決)
行列で一番最初に間違えやすいのが、「どっちが横(行)で、どっちが縦(列)か?」という問題ですが、これは「漢字の形」で覚えるのが正解です。
なぜなら、漢字のつくりそのものが、行と列の方向を表しているからです。これを覚えておけば、試験中にド忘れしても一瞬で思い出せます。
具体的には、上の図のようにイメージしてください。
- 行:漢字の右上の「二」が横線になっているので、横方向。
- 列:漢字の右側の「リ」が縦線になっているので、縦方向。
これで「横が行(Row)」、「縦が列(Column)」と迷わずに判断できるようになります。
行列は「ベクトル」によって定義される
ここまでは「行列=数字の表」というイメージで解説しましたが、ここからがこの記事のハイライトです。実は、線形代数を深く理解している人は、行列を単なる「数字の箱」とは見ていません。彼らは行列を「ベクトルの束(たば)」として捉えています。この視点を持つだけで、今までバラバラに見えていた数式が一気に繋がり、意味を持ち始めます。少し視座を上げて、行列の本当の姿を見てみましょう。
ベクトルとは?(「矢印」であり「数のリスト」)
まず、ベクトルという言葉の定義を考え直しましょう。結論から言うと、ベクトルには「幾何学的な矢印」と「代数的な数のリスト」という2つの顔があります。
なぜなら、文脈によって使いやすい形が変わるからです。しかし、本質的にはどちらも同じ情報を表しています。
例えば、「東に3km、北に4km進む」という情報を考えてみてください。
- 図形で考える場合: 右斜め上に伸びる「矢印」としてイメージします。
- データで考える場合:というように、縦に数字を並べた「リスト(縦ベクトル)」として扱います。行列の話をする時は、後者の「縦に並んだ数字のリスト」としてのベクトルを強く意識してください。
行列は「列ベクトルを横に並べた束(たば)」
ここが最も重要な定義です。行列とは、「いくつかの列ベクトル(縦ベクトル)を、横に並べてひとまとめにしたもの」と定義できます。
その理由は、行列を「個々の数字(スカラー)の集まり」と見るよりも、「情報のまとまり(ベクトル)の集まり」と見たほうが、その構造や役割を理解しやすいからです。
具体的に見てみましょう。
この行列を見たとき、「6個の数字がある」と思うのではなく、「 というベクトルと、というベクトルの、2本のベクトルが並んでいる」と捉えるのです。これが「行列はベクトルによって定義される」という言葉の真意です。
なぜ「ベクトル」で定義すると便利なのか?
なぜわざわざ「ベクトルの束」なんて考え方をするのか?その結論は、「データの管理と処理が劇的にシンプルになるから」です。
理由は、バラバラの数字を一つずつ追うよりも、「意味のあるかたまり」単位で動かしたほうが、全体像を把握しやすくなるからです。
例えば、あるクラスの試験結果を分析する場合で考えてみましょう。
- A君のデータ: 数学・国語・英語の点数(これが1つの縦ベクトル)
- Bさんのデータ: 数学・国語・英語の点数(これがもう1つの縦ベクトル)
これらを横に並べたものが「クラス全体の成績行列」です。こう定義すれば、行列に対する計算は「クラス全員(すべてのベクトル)に対して、一括で同じ処理を行うこと」だと直感的に理解できるようになります。データサイエンスの世界では、この考え方が基本中の基本となります。
3. 【和ベクトル】ベクトルの足し算は「ワープ」である
「和ベクトル(ベクトルの足し算)」という言葉を聞くと、何か特別な計算式が必要だと身構えてしまうかもしれません。しかし、実はこれ、皆さんがRPGなどのゲームや、普段の地図アプリを使った移動で無意識に行っている「ある行動」と同じなんです。ここでは、教科書に出てくる図形的な説明を「移動の近道(ワープ)」という視点で翻訳し、その正体を暴いていきます。難しいことは一切ありません。
図解で翻訳!和ベクトルは「近道」を求めることである
結論から言うと、ベクトルの足し算()とは、「寄り道をせずに、スタートからゴールへ直行すること」です。
なぜなら、ベクトルは「移動」を表す矢印だからです。「$\vec{a}$ 進んでから、続けて $\vec{b}$ 進む」という連続した移動の結果、結局どこにたどり着いたのか?という「最終的な位置の変化」だけを見たものが和ベクトルだからです。これを数学では「平行四辺形の法則」と呼びます。次の項の図も併せてご確認ください。
順番を変えても結果は同じ
次に重要なのは、ベクトルの足し算では「移動する順番を変えても、たどり着く場所は同じ」というルールです。
理由は、寄り道の順序が変わっても、それぞれの方向へ進む距離の合計は変わらないからです。これを図形で表したのが「平行四辺形の法則」です。
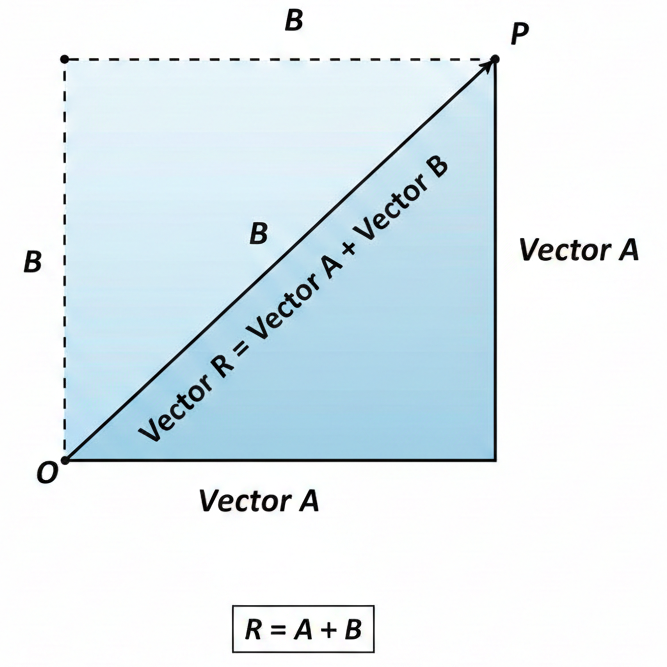
例えば、「東に3歩、北に2歩」進むのと、「北に2歩、東に3歩」進むのでは、歩くルートは違っても、最終的な到着地点は同じですよね。
図を見ると、2つの矢印で作られる平行四辺形の対角線が、和ベクトルになっていることがわかります。これは「」という数式が成り立つことの、視覚的な証明でもあります。
計算の翻訳!「同じ成分同士を足すだけ」
最後に、実際の計算方法を翻訳します。ベクトルの足し算の計算ルールは、「同じ成分(住所)の数字同士を足すだけ」**という非常にシンプルなものです。
なぜなら、横方向(成分)の移動と、縦方向(成分)の移動は、お互いに干渉しない独立した要素だからです。
具体例を見てみましょう。
この足し算は、以下のようになります。
上の階(1行目)同士、下の階(2行目)同士を足すだけ。これ以外の複雑な操作は一切ありません。図形のイメージと計算のシンプルさが結びつけば、和ベクトルは攻略したも同然です。
行列とベクトルの関係性がわかると何が良いのか?
「定義やイメージはわかったけど、実際の計算はもっと難しいんでしょ?」と身構えていませんか?実は、ここまでの内容を理解できた皆さんは、すでに行列の足し算やスカラー倍(定数倍)の仕組みを9割方マスターしています。なぜなら、行列の計算は新しく覚えることではなく、すべて「ベクトルのルールの拡張」に過ぎないからです。最後に、この関係性を理解しておくメリットと、計算ミスを防ぐための重要な視点をお伝えして、実践編へと送り出します。
複雑な計算も「ベクトルのルール」で単純化できる
結論から言うと、行列の計算(和や差)は、「ベクトルの計算を、並んでいる列の数だけ繰り返す作業」です。
その理由は、第2章で定義した通り「行列はベクトルの束」だからです。行列全体を巨大な塊として見るのではなく、分解して考えれば、やっていることは単純な足し算の繰り返しになります。
例えば、行列とを足すという計算があったとします。
これを「の数字を全部どうにかする」と考えるのではなく、「の1列目のベクトルと、の1列目のベクトルを足す」「次に2列目同士を足す」……と考えるのです。
「行列の計算」という新しい公式を覚える必要はありません。「ベクトルの足し算は成分ごと」というルールさえ知っていれば、行列の計算も自然と解けてしまいます。
【注意点】サイズが違う行列は足せない(型の不一致)
行列とベクトルの関係を知っておくと、「足せない行列」を一瞬で見抜けるようになります。
結論として、行列の足し算ができるのは「型(サイズ)が全く同じ場合だけ」です。例えば、行列と 行列は足すことができません。
理由は、ベクトルとして見たときに「対応する相手(相方)」がいない成分が出てくるからです。
3次元のベクトルと、2次元のベクトルを足そうとしても、成分を足す相手がいなくて困りますよね?それと同じことが行列でも起きます。「住所(行数・列数)が一致していないと計算できない」というルールは、単なる暗記ではなく、ベクトルの定義から考えれば当たり前のこととして納得できるはずです。
よくある質問(FAQ)
Q1. 「行列」と「行列式」は似た言葉ですが、何が違うのですか?
行列と行列式は全くの別物です。行列はこれまで解説した通り「数を並べた表そのもの(データの束)」ですが、行列式はその正方行列から計算によって導き出される「たったひとつの数値(スカラー)」です。行列式は、その行列によって変換された図形の面積や体積が何倍になるかという「拡大率」を表す重要な指標ですが、正体は「表」と「値」という決定的な違いがあるため、混同しないように注意しましょう。
Q2. ベクトルの「引き算」はどうイメージすればいいですか?
引き算は「マイナスのベクトルを足す」と考えるとスムーズに理解できます。例えば という計算は、と書き換えられます。は、と長さが同じで向きが真逆のベクトル(逆ベクトル)のことです。つまり、A地点まで進んでから、そこからBベクトルとは逆の方向へ進むルートをイメージすれば、足し算と同じ感覚で答えにたどり着けます。
Q3. 成分がすべて0の「ゼロ行列」には意味があるのですか?
非常に重要な意味があります。ゼロ行列は、普通の数における「0」と同じ役割を果たします。例えば、どんな行列にゼロ行列を足しても元の行列の値は変わりませんし、どんな行列に数字の0を掛けてもゼロ行列になります。これは計算の基準となる存在(単位元のような役割)であり、システムを初期化する際や、方程式の解が存在するかどうかを議論する際などに頻繁に登場します。
Q4. 解説になかった「スカラー」という言葉をよく聞きますが、どういう意味ですか?
スカラーとは、ベクトル(向きと大きさを持つ量)に対して、「大きさのみを持つ普通の数」のことを指します。例えば、風速(向きがある)はベクトルですが、気温(向きがない)はスカラーです。線形代数では、行列やベクトルを単に何倍かする操作を「スカラー倍」と呼びますが、これは「ベクトルを普通の数倍して、長さを伸縮させる」という意味になります。


コメント